数据结构之树的基本概念

在数据结构的世界里，树是一种十分重要且应用广泛的非线性结构。它的形态和我们现实生活中树木的生长形态有着巧妙的相似性，都是从一个 “根” 开始，不断地分支延伸。

一、树的直观认知

现实中的树，从树根生长，然后逐级分支，衍生出树干、树枝、树叶等。数据结构里的树，也是类似的逻辑结构，由一个个节点通过 “边” 连接，形成分层的结构。

二、空树与非空树

（一）空树

空树很好理解，就是结点数为 0 的树，用符号 “∅” 来表示。可以想象成一片没有任何树木的空地，没有任何节点存在。

（二）非空树的特性

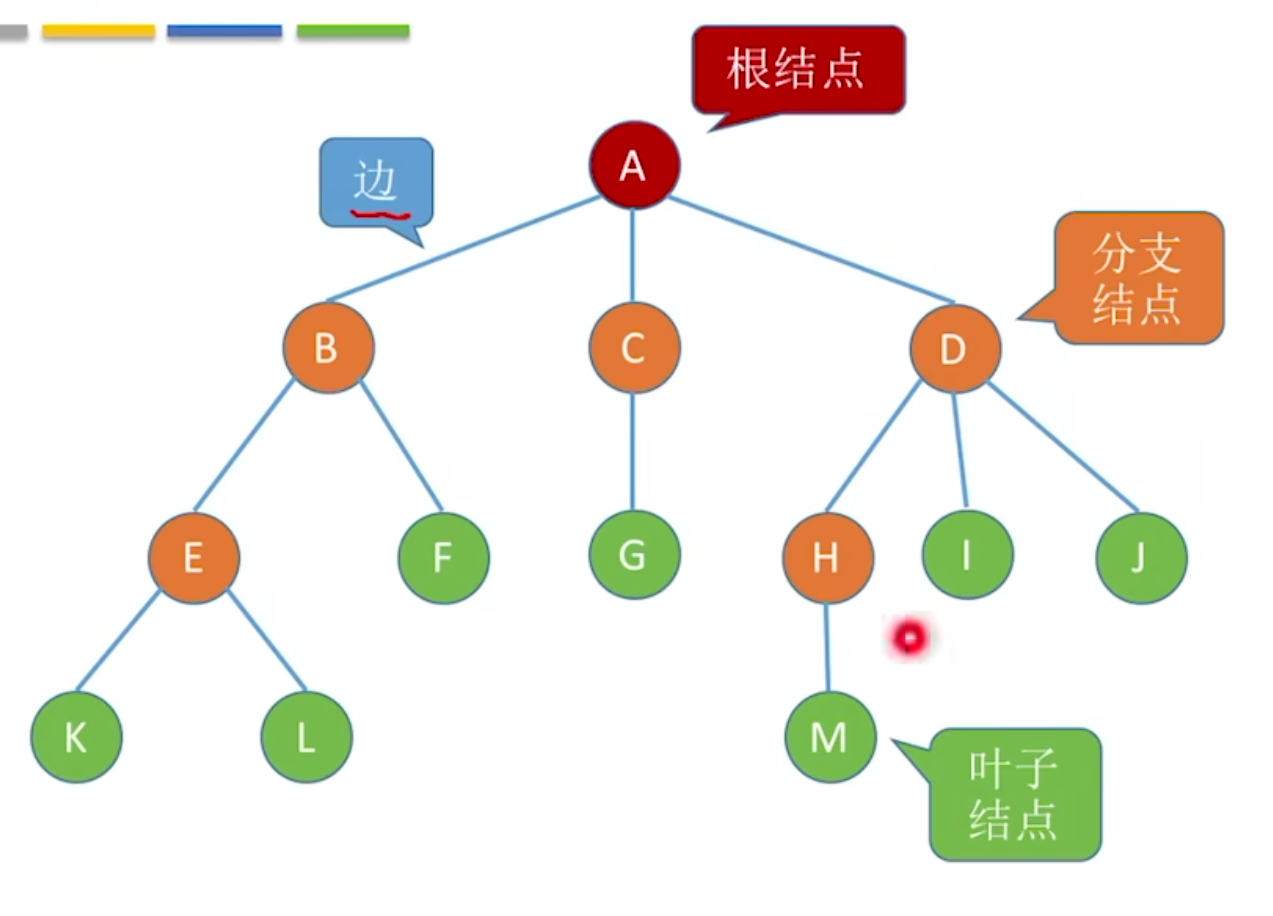
非空树有着几个关键的特性，下面结合示例图（以图中树结构为例，根节点为 A）来详细说明：

1. 根节点的唯一性：非空树有且仅有一个根节点。就像一棵真正的树只有一个树根一样，数据结构里的树也只有一个 “根”，图中的根节点就是 A，所有的节点都直接或间接从它衍生而来。
2. 叶子结点（终端结点）：没有后继的结点称为 “叶子结点”。比如图中的 F、G、K、L、I、J、M，它们处于树的末端，没有再分支出去的节点，就像树木最末端的树叶。
3. 分支结点（非终端结点）：有后继的结点称为 “分支结点”。像图中的 B、C、D、E、H，它们都有后续的节点，起到了分支连接的作用，类似树木的树干、树枝部分。
4. 前驱的唯一性（除根节点外）：除了根节点外，任何一个结点都有且仅有一个前驱。例如 B 的前驱是 A，E 的前驱是 B，这保证了树结构中节点连接的有序性，每个节点（除根外）都只有一个 “来处”。
5. 后继的多样性：每个结点可以有 0 个或多个后继。比如根节点 A 有 B、C、D 三个后继，而叶子结点 F 则有 0 个后继，这体现了树结构分支的灵活性。

三、结点的度与树的度

（一）结点的度

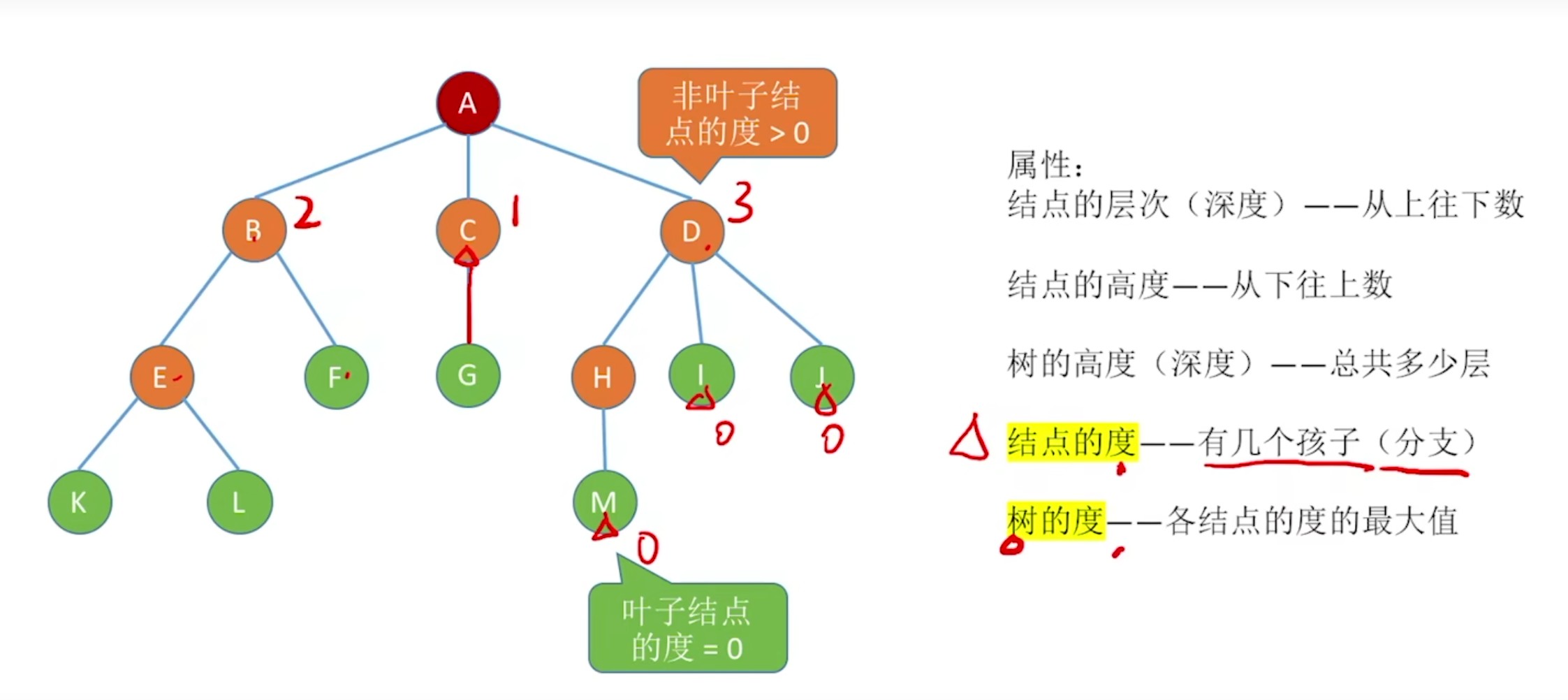
结点的度指的是该结点有几个孩子（分支）。比如在图中：

• 结点 B 有 2 个孩子（E 和 F），所以结点 B 的度是 2。
• 结点 C 有 1 个孩子（G），所以结点 C 的度是 1。
• 结点 D 有 3 个孩子（H、I、J），所以结点 D 的度是 3。
• 像叶子结点（如 F、G、K、L、I、J、M），它们没有孩子，所以度为 0，这也符合 “叶子结点的度 = 0” 的特性；而非叶子结点（如 B、C、D、E、H），它们都有孩子，所以 “非叶子结点的度 > 0”。

（二）树的度

树的度是各结点的度的最大值。观察图中的各个结点，结点 D 的度是 3，结点 B 的度是 2，结点 C 的度是 1，其他结点度更小，所以这棵树的度是 3。

四、有序树与无序树

（一）有序树

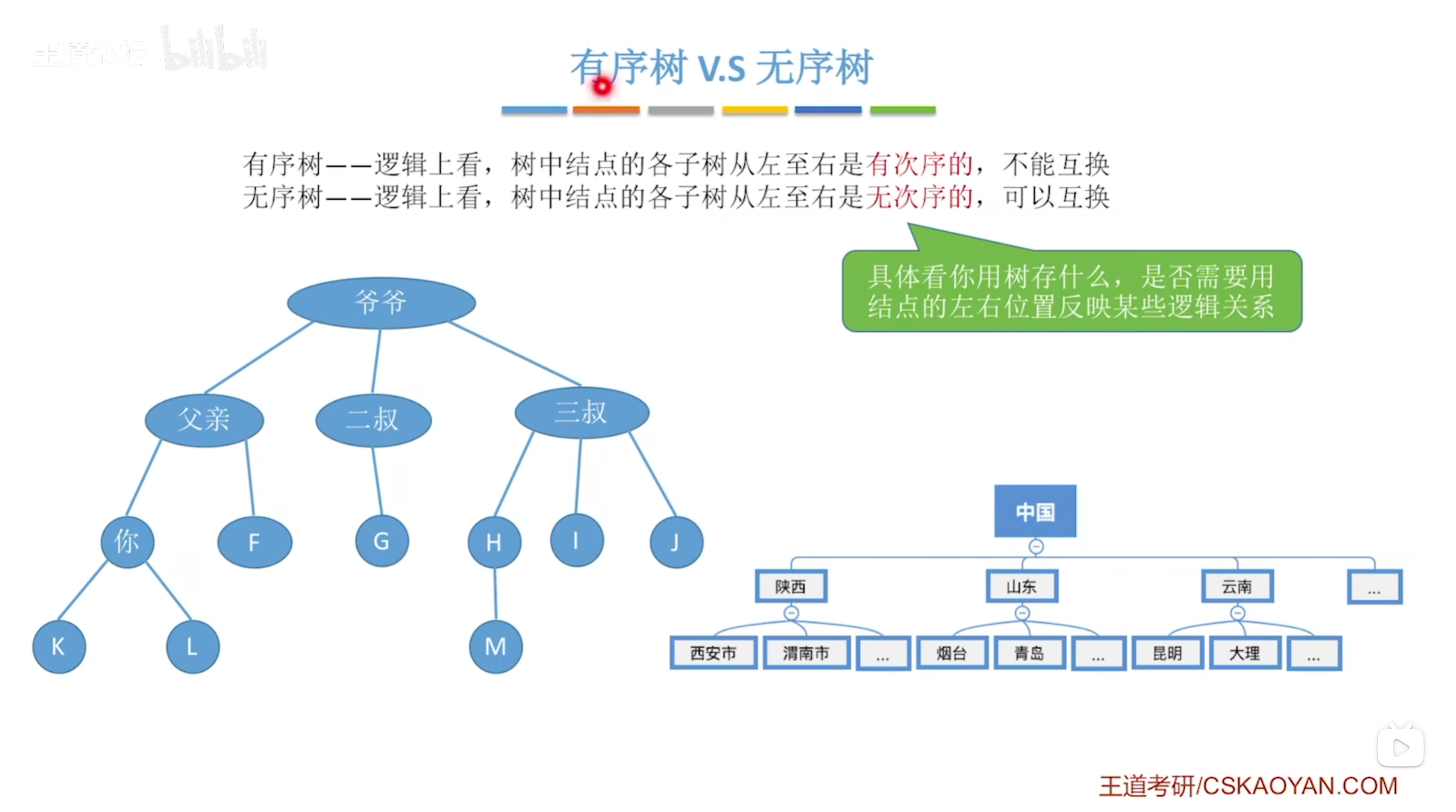
有序树的特点是，从逻辑上看，树中结点的各子树从左至右是有次序的，不能互换。比如图中的家族树，“爷爷” 的子树 “父亲”“二叔”“三叔” 是按长幼顺序排列的，这种顺序是有意义的，不能随意调换；还有中国行政区划树，“中国” 下的 “陕西”“山东”“云南” 等子树，是按照一定的行政或地理逻辑有序排列的，调换顺序就会破坏原本的逻辑关系。

（二）无序树

无序树则是，从逻辑上看，树中结点的各子树从左至右是无次序的，可以互换。

（三）如何区分使用

具体看用树存储什么数据，是否需要用结点的左右位置反映某些逻辑关系。如果子树的顺序承载了特定的逻辑，比如家族的长幼、行政区划的类别等，那就是有序树；如果子树顺序不影响逻辑表达，就可以视为无序树。

有序树和无序树的区分，能帮助我们更精准地根据实际需求选择合适的树结构来组织数据，确保数据的逻辑关系得到正确的体现。

五、树的性质：结点数与总度数的关系

在树的结构中，有一个非常重要且常见的考点：结点数 = 总度数 + 1。

首先回顾 “结点的度” 的概念，结点的度是指该结点有几个孩子（分支）。那为什么会有 “结点数 = 总度数 + 1” 这样的关系呢？

我们可以这样理解，树中的每个分支（也就是结点的度所对应的孩子连接），都连接着一个子结点。总度数就是所有结点的度之和，它代表了树中分支的总数。而树的根节点是没有父结点的，除了根节点之外，每个结点都有且仅有一个父结点，这就意味着每个非根节点都对应着一个分支。所以，分支的总数（总度数）就等于结点数减去 1（因为根节点没有通过分支来自其他结点），反过来就是结点数 = 总度数 + 1。

以图中的树为例，我们来验证一下：

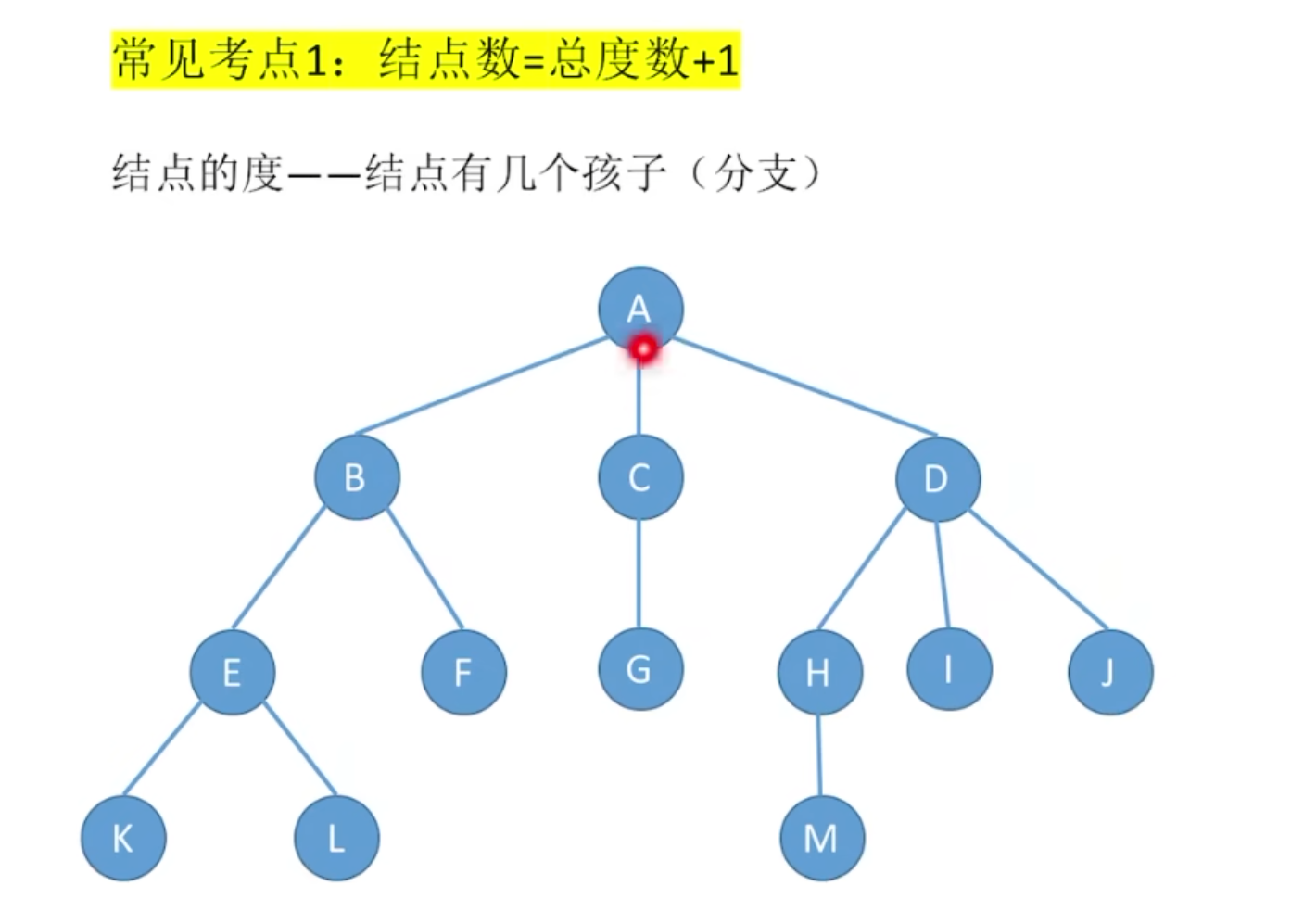
• 先看各个结点的度：
  • 结点 A 的度是 3（有 B、C、D 三个孩子）。
  • 结点 B 的度是 2（有 E、F 两个孩子）。
  • 结点 C 的度是 1（有 G 一个孩子）。
  • 结点 D 的度是 3（有 H、I、J 三个孩子）。
  • 结点 E 的度是 2（有 K、L 两个孩子）。
  • 结点 H 的度是 1（有 M 一个孩子）。
  • 结点 F、G、I、J、K、L、M 的度都是 0（没有孩子）。
• 计算总度数：3+2+1+3+2+1+0+0+0+0+0+0+0=12。
• 数一下图中的结点数，一共有 13 个结点（A、B、C、D、E、F、G、H、I、J、K、L、M）。
• 验证公式：总度数12+1=13，正好等于结点数。

这个性质在解决很多与树的结点数量、分支数量相关的问题时非常有用，是树结构的一个基础且关键的特性。

六、度为m的树与m叉树的区别

在树的相关知识里，度为m的树和m叉树是两个容易混淆但又有明显区别的概念，这也是数据结构中的常见考点，下面我们来详细区分它们。

（一）核心定义回顾

• 树的度：各结点的度的最大值。
• m叉树：每个结点最多只能有*m个孩子的树。

（二）具体区别

特性	度为m的树	m叉树
结点度的上限	任意结点的度≤m（最多m个孩子）	任意结点的度≤m（最多m个孩子）
是否存在度为m的结点	至少有一个结点度=m（有m个孩子）	允许所有结点的度都<m
树的空非特性	一定是非空树，至少有m+1个结点	可以是空树

（三）示例理解

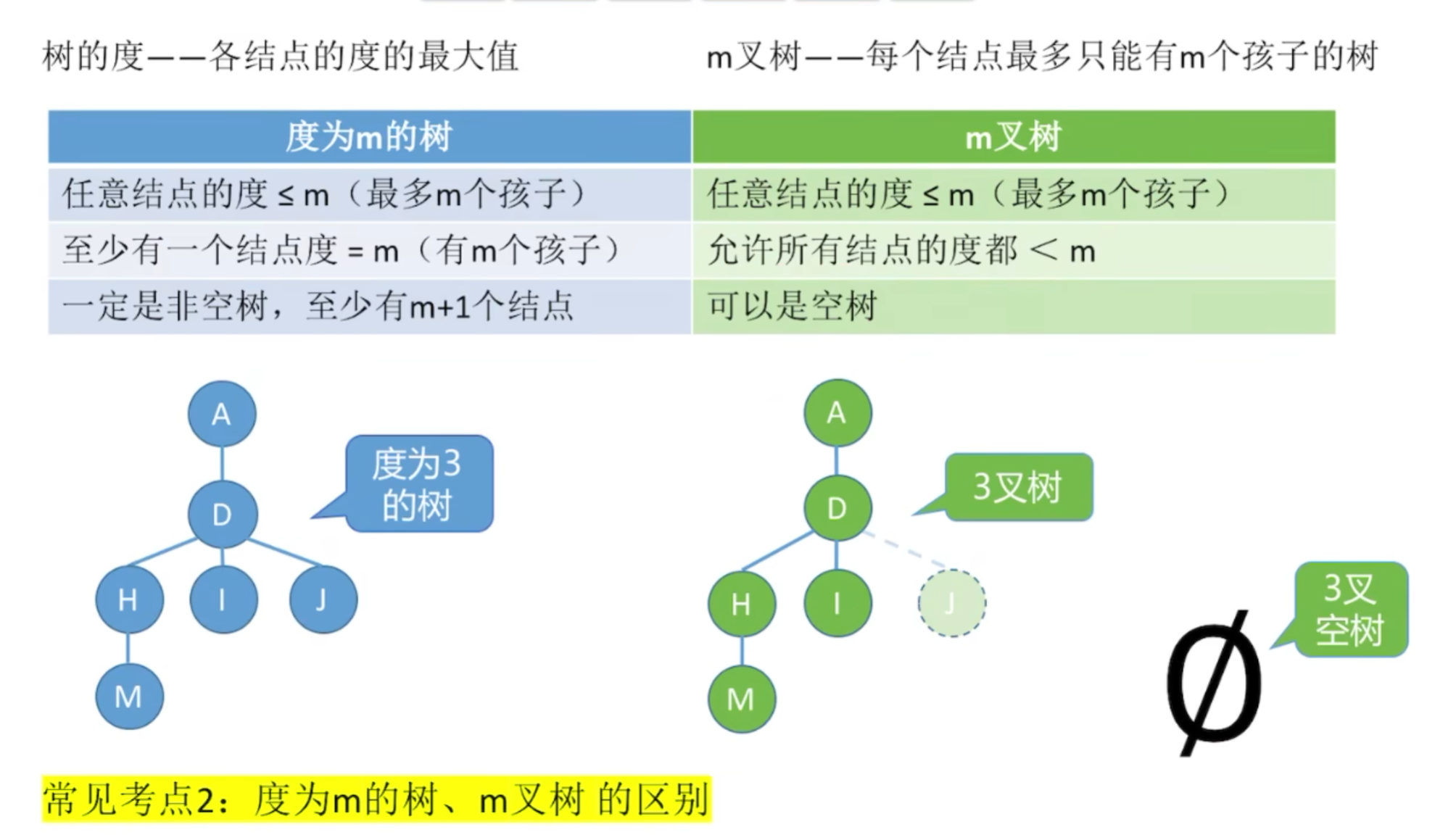
• 度为3的树：如图中左侧蓝色树结构，结点D的度为3（有H、I、J三个孩子），满足 “至少有一个结点度=m（这里m=3）”，并且这棵树是非空的，结点数量也符合 “至少有m+1=4个结点”（实际有多个结点）。
• 3叉树：如图中中间绿色树结构，结点D最多可以有3个孩子，但实际孩子数量少于3（有H、I，虚线的J可理解为允许存在但未实际生成），而且还存在右侧的 “3叉空树”（用∅表示），这都体现了m叉树 “允许所有结点的度都<m” 以及 “可以是空树” 的特点。

清楚区分度为m的树和m叉树，对于后续学习树的各种操作、分析树的结构等都至关重要，能帮助我们更准确地把握不同树结构的特性与适用场景。

• 对于度为m的树，第i层（i≥1）至多有m**i−1个结点。
• 对于 m叉树 **，第i层（i≥1）至多也有m**i−1个结点。

以图中类似3叉树的结构为例，第1层有m0=1个结点（根节点）；第2层至多有m1=3个结点；第3层至多有*m*2=9个结点；第4层至多有*m*3=27个结点，以此类推。这一规律体现了在度为*m*的树和*m*叉树中，每一层结点数量的上限是按照指数规律增长的。